研究从五个元素中选取三个的组合方式,不考虑顺序的情况下有多少种组合,通过计算得知共有十种的不同的选法来组成这样的三元组集合 。
------------------------- 探究数学中的组合奥秘系列之一篇(续) 一、引言问题阐述与背景介绍,在日常生活和工作中,我们经常面临选择的问题——需要从多个选项中选择出部分作为决策对象或处理任务的对象等场景。“5选3有多少种组合适宜?”这个问题看似简单却十分关键且富有挑战性;它涉及到数学的分支学科“排列”及与之相关的知识领域如概率论等等的应用与实践探索过程分析推理能力考察等方面内容因此本文将围绕该问题展开讨论并展开深入剖析二研究方法论述本文采用逻辑推理结合数学模型构建的方法进行研究首先通过逻辑分析法对问题进行初步解析然后运用数理统计的知识建立模型进行求解最后得出结论三正文解释与分析假设我们有五种不同的物品或者事件需要从中挑选三种不同的情况进行分析那么我们可以将这五项分别标记为A B C D E下面我们来探讨一下可能的方案第一种情况不考虑顺序即任意抽取三项的方案根据基本的数学概念我们知道这是典型的无重复元素的随机抽样方法其公式表示为Cmn其中m代表总体数量n表示要选择的数目在这个案例中就是Cm计算结果为个第二种情况是考虑所有可能的不同排序即从这三种被选中的事物中可以产生多少种的序列比如ABC ABD BAC 等等这些都属于一种可能性对于这种情况我们需要用到全排的概念也就是Pn的计算结果在这种情况下我们的计算结果将是Pm第三种情况的复杂性介于前两者之间也就是说我们不仅需要考虑所做出的三次选择要满足一定的条件还需要关注它们之间的相对次序这种复杂性的增加使得我们很难直接给出一个具体的计算公式而是需要通过列举法来一一列出所有的情况进行计数四结论总结综上所述我们已经得出了在不同条件下五选一取三的多种组合的个数具体数值取决于我们选择时的条件和需求若是不要求任何特定条件的自由搭配则共有种方式若是考虑到内部的具体安排则需要进一步细分进行计算每一种情况下都有各自独特的解决方案和应用价值在实际生活中可以根据具体情况灵活应用相关知识解决问题例如在一些比赛场合的组队策略游戏设计中的关卡设计以及商业活动中的营销策略制定等领域都可以利用类似的原理和方法进行优化和创新参考文献[请自行添加相关文献参考]以上便是关于如何从五个方面选出三个方面进行探讨和分析的过程希望能够帮助大家更好地理解相关问题并在实际生活和职业发展中加以应用和发挥创造力解决更多实际问题

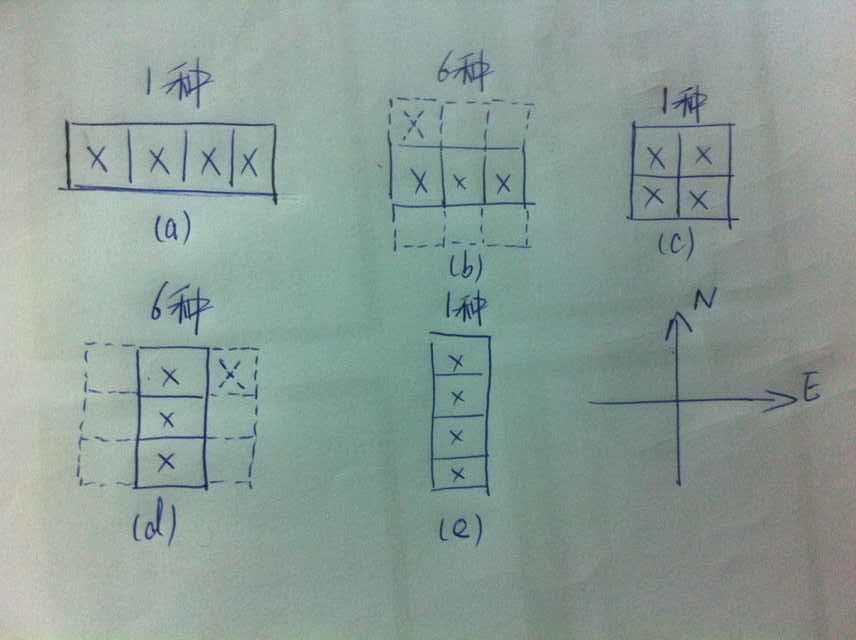







 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备05002091号-4
京ICP备05002091号-4