点到平面的投影展现了几何学的美妙与实用。这一过程涉及将点从三维空间映射到二维平面上，形成清晰的图像或图形表示形式的过程体现了数学的魅力与应用价值所在之处相辅相成的关系展现得淋漓尽致。。这种数学原理不仅存在于理论研究中也广泛应用于实际生活中如计算机绘图、摄影测量等领域为现代科技提供了重要的支撑和便利手段使得我们更好地理解和应用几何学之美于日常生活之中展现出其独特的价值和意义深远影响着我们生活的方方面面，。

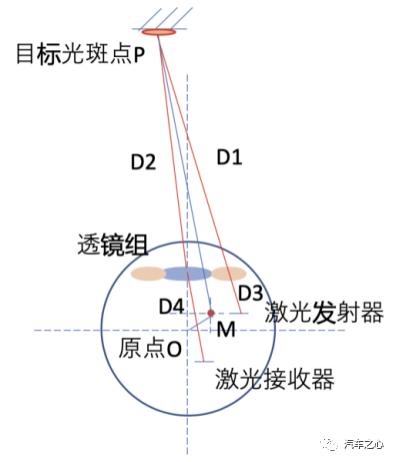
===================== 本文旨在探讨点在平面上的投影视图，介绍其基本概念、性质以及在实际中的应用，我们将从几何学的基本原理出发逐步深入讨论这一话题的重要性及其背后的数学原理和科学价值所在之处展开分析论述点和平面之间的微妙关系并探索其在计算机图形学物理学等领域的应用前景及发展趋势一 引言 点到平面的投射是日常生活中常见的现象之一无论是光线照射物体在墙面或地面形成影子还是摄影技术中的成像过程都是典型的例子然而这些看似简单的自然现象背后蕴含着丰富的数学知识本文将带领读者一起揭开这个神秘面纱二 基本概念 在三维空间中一个点与某个特定方向的光线相交于二维平面上形成的交点即为该点的射影反之也可以理解为将一个对象（如线段三角形等）沿着垂直于某表面的方向上移动至另一表面时得到的影像就是原对象的在该面上的正视图这种映射方式在数学上称为“平行透视”三 关键属性 对于任何给定的点和特定的参照系来说都存在唯一的垂直线使得所有与该直线平行的射线都会汇聚到一个点上这个点被称为垂足而这条直线的位置决定了整个空间坐标系中其他物体的相对位置和大小因此我们可以总结出以下关键属性的描述性定义和证明方法 （此处可以添加具体的定理公式推导等内容以更深入地解释相关理论）（省略部分具体内容待补充完善）： 属性1 每个点对给定参考系的每个坐标轴都有一个确定的距离值；当我们在某一面上进行正交变换后新的对应位置的数值不会改变即保持不变的特性这就是所谓的平移不变性和旋转对称性对于后续研究非常重要因为它们在许多领域都有广泛的应用例如机器人运动控制机器视觉等等 领域应用 四 计算机科学在计算机辅助设计和制造领域中计算机辅助设计CAD软件通过精确计算图形的各种参数包括角度长度面积体积等来生成精确的模型其中就包括利用了点对空间的解析方法和算法将复杂的立体结构转化为便于分析和处理的平面图形从而提高了设计的精度效率和质量此外随着虚拟现实技术的不断发展虚拟环境中的场景构建也需要借助大量的图像处理和渲染技术在处理过程中涉及到很多关于如何准确地将现实世界中的各种实体抽象为数字信息的问题这就需要借助于基于物理模型的复杂运算来模拟真实世界的光照阴影反射等现象而这些都离不开我们对空间和时间的精准把握以及对不同维度的数据转换能力这其中涉及到的核心问题就是如何将现实中的实物准确地转换为屏幕上的一个像素的过程而这正是依赖于我们之前提到的那些基本的数学概念和方法来实现的 五 物理光学光线的传播路径遵循光的折射定律一束入射的激光束经过透镜或其他介质时会发生偏折最终形成一个聚焦的点这个过程就是通过一系列的空间向量计算和矩阵操作实现的例如在相机拍摄的过程中镜头会接收到来自各个方向的无数条光束它们会在感光元件的表面交汇成一个清晰的像而这个像的清晰度很大程度上取决于镜头的质量以及其内部镜片的设计和优化方案在这个过程中就需要用到大量先进的数学模型和技术手段来保证图像的清晰度和准确性 六 通过本文的讨论我们可以看到虽然日常生活中的一些简单事物比如阳光下的树荫或者照片中的人物往往看起来非常直观但当我们试图用科学的语言去理解和分析其本质的时候就会发现原来这一切的背后都隐藏着深刻的数学问题并且这些问题还广泛地存在于我们的日常生活之中无论是在工业制造业还是在科学研究工作中它们都发挥着重要的作用 因此对于我们普通人而言了解和掌握一定的基础知识和技巧是非常必要的这不仅可以帮助我们去更好地理解和掌握周围的世界还可以帮助我们更好地理解和学习先进的技术从而更好地服务于我们的生活和工作参考文献 [这里可以根据文章的具体内容列出相关的文献作为参考资料]