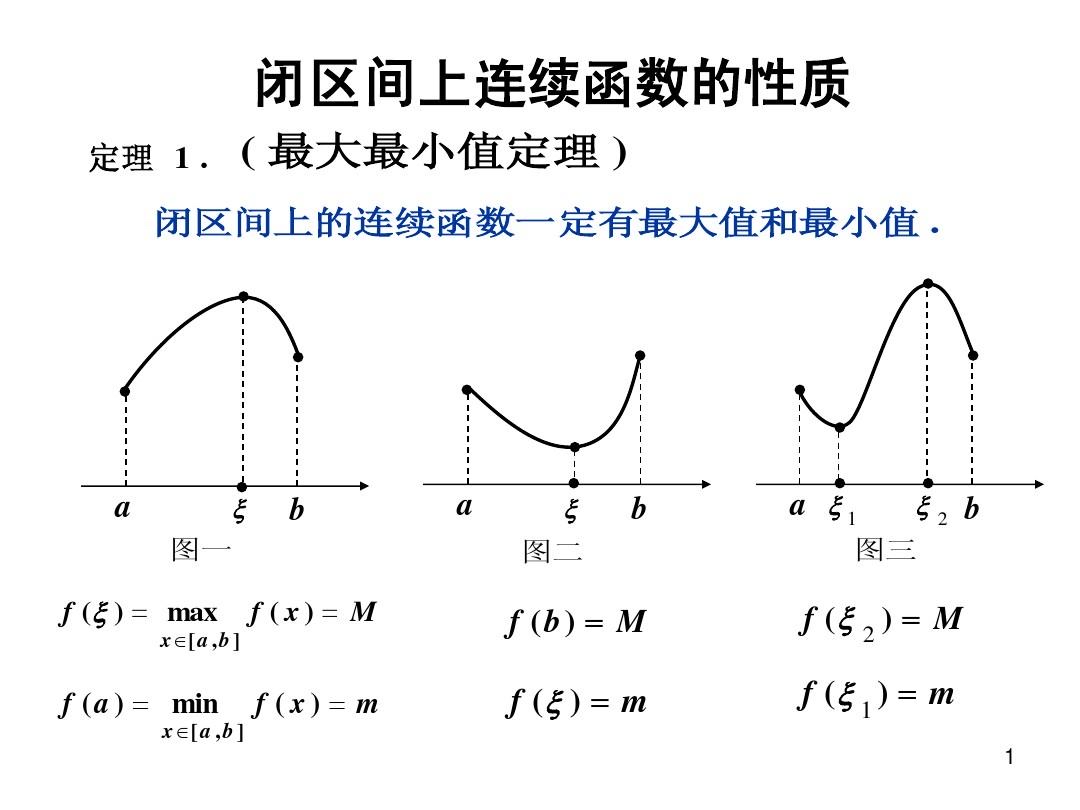
连续函数介值定理是数学中的一项重要理论，作为连接不同数学概念之间的桥梁与纽带。它揭示了函数的连续性与其在区间内取值之间的关系：对于给定的两个实数端点上的数值差异较大的情况下存在至少一个中间值的性质得以证明和解释的过程正是通过这一原理实现的突破性的进展使得该定律在数学领域具有广泛的应用价值并促进了数学的进一步发展与应用推广起到了重要的推动作用

======================= 走进数学的奇妙世界，我们总会遇到许多令人着迷的定律和理论。“连读函数的介质数值原理”（即“连续性区间内任意值的性质”）是一个极其重要的概念之一。“连续的”意味着一个变量在某一范围内变化时其值是平滑变化的；“中介性质”，则是指在一个特定的范围或集合中某个特定性质的保持状态；而所谓的"定理解释"，则是对于这一性质和现象的数学化描述和理解方式的具体阐述。"这个重要的命题不仅为我们提供了对实数轴上的某些特性的深入理解,而且也为解决更复杂的数学问题打下了坚实的基础。”接下来我们将深入探讨这一主题的内涵及其在数学领域的应用价值等各个方面的问题展开论述分析工作介绍给大家参考学习之用目的所在之处一探究竟吧！ 一、连续 函数的基本认识 在谈论到任何有关实数的复杂问题时，"延续性的功能"（continuous function）无疑是我们需要首先了解的概念 ，所谓 "持续的功能",就是指当自变量在一定范围之内改变的时候 ,因变量的取值也会相应地发生一种规律的变化 ，这种变化规律呈现出十分平稳的状态特性来表现出来的一种特征属性表现形态或者称之为特点等等方面内容的表现情况表述出来的一个数学概念定义范畴之内所涵盖的内容信息点之重要一环组成部分要素构成单元结构体系框架之中不可或缺的重要基础元素组成成分之一的内涵和外延表达形式呈现出来的基本认知过程以及应用实践过程中所需要掌握的核心知识点二 、 理解 “介入定值法则 ” 的核心思想 当我们在探讨持续性功能的各种属性和特质之时往往会遇到一个非常有趣而又十分重要的概念和观点——“介于中间的值”，这个概念是借助于直观想象和实际应用的经验总结而来的一个非常具有启发性和指导意义的结论或者说是公理假设它告诉我们当一个具有一定范围的数集被映射到一个新的可接受的区域中时在这个新区域内必定存在着至少一个在某种意义下能够代表整个原始数据集中所有元素的代表性数字或者说是一种特殊的平衡点它的存在使得我们可以将问题简化并找到解决方案这就是我们所要介绍的第二个核心概念——也就是著名的插入固定规则（也称为插入零点原则）。 三、“连接法规定理”：从抽象走向具体 通过上述两个概念的铺垫我们已经可以清晰地看出它们之间的联系以及在解决问题时的巨大作用那么如何将这两者结合起来形成一个更加完整且实用的理论体系呢？这就引出了我们今天的主角 —— 连接法的恒定理念通过该理念的引入我们能够把看似抽象的数学模型转化为实际生活中可见的现象从而帮助我们更好地理解和运用这些知识和方法具体来说就是当我们面对一些涉及到多个不同区间的复合性问题时可以借助此一定律进行逐步分析和推理找出问题的关键节点进而得出正确的答案四、"链接法定论的实际应用价值通过以上几个部分的讨论相信大家对连结法在解决实际问题方面的价值和重要性已经有了比较深刻的认识然而这只是冰山一角在实际应用中还有许多值得我们去挖掘和探索的领域例如微积分学极限计算最优化问题等都可以利用此一工具来解决这些问题往往涉及大量的计算和逻辑推理如果没有强大的理论基础作为支撑很难取得实质性的进展而通过联结法的规定我们可以在一定程度上避免繁琐的计算同时提高解题效率为科研人员提供更加高效的研究手段五结语综上所述我们可以看出联接法对研究和分析现代科学特别是物理学化学工程学等领域起到了至关重要的作用它不仅解决了大量实际问题同时也极大地推动了相关学科的发展未来随着科技的进步和应用领域的不断拓展将会有更多的新问题涌现而出此时我们更应该充分利用好联络法规这把利器不断拓宽我们的知识视野深化对它的理解和掌握以便能够更好地服务于社会和人类发展最后让我们共同期待更多有志之士投身于此项伟大事业中去共创辉煌明天参考文献：[请在此处添加相关的专业书籍文献等资料]